§25   正定二次型与正定阵

　　    在这一节，我们只讨论实二次型。

　　 定义25.1 　设f(X)= X AX 是ｎ元实二次型，对任意一组不全为零的实数 　　

     （１）如果总有ｆ ( ) ＞０，那么这个二次型称为正定型；

　　（２）如果总有ｆ ( ) ≥０，那么这个二次型称为半正定型；

　　（３）如果总有ｆ ( ) ＜０，那么这个二次型称为负定型；

　　（４）如果总有ｆ ( ≤０，那么这个二次型称为半负定型；

　　（5 ）如果二次型ｆ ( ) 既不是半正定的又不是半负定的，那么这个二次型称为不定型；

　　特别，当实二次型 f(X)=X AX 是正定型时，它对应的实对称矩阵Ａ称为正定阵。

　　给出一个实二次型，如果它是标准形，那么它是正定型当且仅当它的ｎ个平方项的系数全大于零，否则，就不容易判断它是否为正定型了。

　　引理 25.1 　可逆变量替换保持实二次型的正定性不变。

　　因此，我们容易证明下面的判定定理。

　　定理 25.2 　设f(X)= X AX 是ｎ元实二次型，则下述命题等价：

（１）f(X)= X AX 是正定型，从而对应的实对称矩阵 A

（２）X AX>0 对所有的不为零的Ｘ＝ 　 R 成立；

（３）实对称矩阵 A 的所有特征值 全正；

　　（４）实对称矩阵 A 与单位矩阵Ｅ合同；

　　（５）实二次型 X （-A ）X 是负定型。

　　我们把证明作为习题留给读者。

　　最后我们要介绍一个非常具体的法则来判别一个实对称矩阵是否为正定阵，但不给出证明。

　　定理 25.3   ｎ阶实对称矩阵Ａ＝（ ）为正定阵的充分必要条件是Ａ的各阶主子式全为正，即

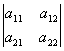＞0 , 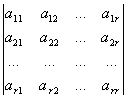   ＞0 ,  >0,   

ｎ阶实对称矩阵Ａ为负定阵的充分必要条件是Ａ的各奇数阶阶主子式全为负而偶数阶主子式全为正，即

       >0     ， r=1,2,.......,n  .

利用实对称矩阵的正定性，可以判断多元函数的极大值与极小值，根据多元函数的泰勒（ Tylor ）展开式

　　　ｆ（ X + ΔX )=f （X )+( ΔX ) +( ΔX) A( ΔX )+R

其中

 , ΔX =    ,                        

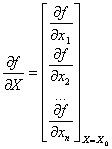
       A=

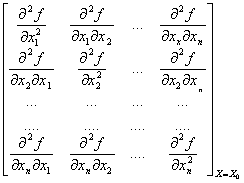
如果Ｘ＝Ｘ 是极值点，那么一定有 , 这时有

在的足够小的邻域内，上是右端的正负号由二次型

  决定，当Ａ是正定的实对称矩阵时， f(X) 在X=X 处取极小值；当Ａ是负定的实对称矩阵时， f(X) 在X=X 处取极大值。