§23  二次曲面及其分类

　　 上节指出，实对称矩阵一定可以正交相似于一个对角阵，应用这个事实，我们来研究二次曲面（二次曲线）的分类问题。

　　在空间直角坐标系 O-XYZ 下，二次曲面的一般方程是

         Φ(x,y,z)=ax +by +cz

               +2dxy+2exz+2fyz+2gx+2hy+2kz+L=0     (23-1)

令

            A= ，X = ，C = ，

式 (23-1) 可以写成矩阵方程的形式

               (X)=X AX+2C X+ =0                (23-2)

　　我们知道对于实二次型 X AX=ax +by +cz +2dxy+2exz+2fyz ，可以经过正交的变量替换 X=TX ， 化为标准形λ x + λ y + λ z ,

其中，系数是实对称矩阵 A 的全部特征值， X = .   这里所作的正交的变量替换，实际上是把空间直角坐标系 O-X Y Z 旋转到二次型 X AX 的主轴上，得到新的直角坐标系 O-X Y Z 使二次型变为标准形。这就是通常所说的直角坐标系的旋转变换。当 |T|=1 时，它把右手系变到右手系；当 |T|=-1 时，它把右手系变到左手系。因此我们在作直角坐标系的旋转变换化简二次曲面方程时，总要求所涉及的正交阵 T 的行列式为１，现在式 ( 23-2) 可以化为

           X (T AT)X +2( C T)X + =0             (23-3 ）

进一步记(b ,b ,b )=C T ，上式可以改写为

                (23-4)

由于R(A)=R( T AT) ，R(T AT) 就是不为零的特征值 (i=1,2,3) 的个数，我们可以根据 R(A) 把二次曲Φ(x,y,z)=0 面进行分类。

1． R(A)=3 时, 通过直角坐标系的平移 X =X +D, 其中

X =   , D= ,

式（23-4 ）化为 

                             (23-5)

其中，r= - .

　　（１）ｒ＝０时，二次曲面方程表示一个锥面。如果 λ ，λ ，λ ，不全同号，这是一个椭圆锥面。特别当λ ＝λ 与λ 异号时，这是一个圆锥面，即在空间直角坐标系中，直线绕轴旋转一周而成的圆锥面。如果λ ，λ ，λ ，同号，它退化为一点。

　　（２）　ｒ≠０时，按 λ ，λ ，λ 与ｒ的符号分以下四种情况：

　　（ａ）当λ ，λ ，λ 都与ｒ异号时，这是一个虚椭球面；

　　（ｂ）当λ ，λ ，λ 都与ｒ同号时，这是一个椭球面；

　　（ｃ）当λ ，λ ，λ 有两个与ｒ异号时，这是一个单叶双曲面；

　　（ｄ）当λ ，λ ，λ 有两个与ｒ同号时，这是一个双叶双曲面；

　　特别当中有两个相等时，这是一个旋转曲面，在（ａ），这是一个旋转椭球面；在（ｃ），这是一个旋转单叶双曲面；在（ｄ），这是一个旋转双叶双曲面。

　　２。 R(A)=2 时，不妨设λ =0 ，式（23 －４）化为

                        ( 23-6)                                                          

通过直角坐标系的平移 X = X +D ，其中

                X =   ,  D=

式（２３－６）化为

                                             （23.7 ）

其中，ｑ＝        

　　（１）b =q=0 时，二次曲面方程式（ 23 －１）表示一对相交的平面。如果λ 与λ 同号，这是相交于实的一对虚的平面，如果λ 与λ 异号，这是一对实的相交平面。

（２）b =0 但q ≠ 0 ，二次曲面方程式（ 23 －１）表示一个柱面，如果λ , λ 与q 同号，这是一个虚的柱面；如果λ , λ ,q 不全同号，只是一个实的柱面。特别，当λ , λ 同号时，这是一个椭圆柱面；当λ 与λ 异号时，这是一个双曲柱面。

　　（３）b ≠ 0 时，进一步作直角坐标系的平移 X = X +G ，其中

                      X = ,G=

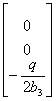
式（２３－７）化为

                                                (23-8)

  这时，二次曲面方程式（２３－１）表示一个抛物面，如果λ 与λ 同号，这是一个椭圆抛物面；如果λ 与λ 异号，这是一个双曲抛物面。特别，当λ = λ 时，这是一个旋转抛物面，即在坐标平面 Z O X 上的抛物线 绕Z3 轴旋转而成的曲面 .

３。R(A)=1 时，不妨设λ ≠ 0 ，λ = λ =0 式（２３－４）化为

                                   (23-9)

  通过直角坐标系的平移：

                       X = X +D

其中               X = ,    D=

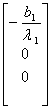
式（２３－９）化为

                               （ 23-10 ）

其中, ｐ＝l- .

（１）b =b =0 时，二次曲面方程式（２３－１）表示一对平行平面。如果λ 与p 同号，这是一对虚的平行平面。如果λ 与p 异号，这是一对实的平行平面；如果 p=0 ，这是一对重合的平面。

　　（２）b 或b 至少有一个非零时，进一步作直角坐标系的旋转与平移：                                      

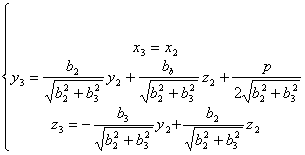
式（23 －１０）化为

                                             ( 23-11)

这时，二次曲面方程式（２３－１）表示一个抛物柱面。

　　如果我们仔细考察锥面、柱面、单叶双曲面、和双叶双曲抛物面的方程的标准形，发现有些直线都在曲面上，我们把这样的直线叫做所在曲面的 直母线。

  对于柱面  而言，在XOY 坐标平面上的椭圆    双曲线 和抛物线 称为对应柱面的准线，一般说来，沿着定曲线Ｃ（柱面准线）移动且平行于定直线的直线 的轨迹称为柱面。

　　最后我们讨论两个曲面的交线－－空间曲线。设空间曲线Ｃ是两个曲面Φ (x,y,z)=0 和Ψ(x,y,z)=0 的交线，那么，Ｃ上任意一点的坐标满足方程组

                          ,

并且坐标满足方程组的点一定在空间曲线Ｃ上。