§18   线性空间的同构

      设V 是数域F 上的    n 维线性空间,   ， ，…， 是它的一个基。由上节可知，对任意的α，β V, 它们在这个基下有唯一确定的坐标

α = （   ， ，…， ）   ，β= （   ， ，…， ）          。

于是，对任意的λ F, α+ β= （   ， ，…， ）        ,

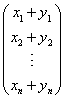                   α= （   ， ，…， ）         .

这样，可以在线性空间 V 与有序  n 元素组所张成的向量空间 之间建立起一个一一对应  :V   , 使   =            .

显然，影射   还保持了线性空间 V 与 的线性运算关系，即

                 =   +

                   =λ .

我们把具这些性质的映射      称为从线性空间 V 到   上的同构映射，一般说来，有

    定义18.1   设   ,   是数域F 上的两个线性空间，如果从 到 有一个映射    ：   , 满足

    (1)     是从 到   上的一一映射；

    (2) 对任意的α，β    , 有 =   +

    (3) 对任意的α   V  ，任意的    F, 有   =λ .

那么， 是从 到   上的同构映射 。如果两个线性空间之间存在一个同构映射，就称这两个线性空间同构。

    前面的论述证明了下面的定理。

    定理18.1    数域F 上任意一个 n   维线性空间V 和数域F 上有序   n 元数组的向量空间 同构。

    进一步可知，线性空间的同构具有下述性质：

    (1) ,   

    (2)    

    (3)  设   ：     是线性空间 到 上的同构映射，那么 中的向量组   ， ，…，   线性相关当且仅当它们在 中的像 , , …, 线性相关。

     (4)  同构的线性空间的维数相等，反过来，维数相等的线性空间都同构。