§9 线性相关与线性无关
教学要求 ： 掌握线性相关与线性无关的定义,并能够判断向量组的线性相关性
知识要点 :
一、 定义与例子 :
定义
9.1
对向量组
，如果存在一组不全为零的数
,
使得
那么,
称向量组
线性相关.
如果这样的
个数不存在,
即上述向量等式仅当
时才能成立,
就称向量组
线性无关.
含零向量的向量组
一定线性相关
,
因为
其中,
不全为零.
只有一个向量
组成的向量组线性无关的充分必要条件是
,
线性相关的充分必要条件是
.
考虑齐次线性方程组
(*)
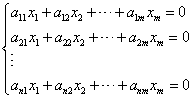它可以写成
，
或
,
其中
.
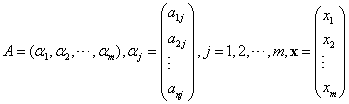由此可见,
向量组
线性相关的充分必要条件是齐次线性方程组
(*)
有非零解.
也就是说,
向量组
线性无关的充分必要条件是齐次线性方程组
(*)
只有零解.
例1
向量组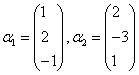
是线性无关的
.
解:
设有
使
,
即
,
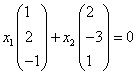得齐次线性方程组
.
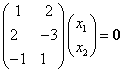解此方程组得
,
所以向量组
线性无关.
例2
设向量组
线性无关,
又设
,
证明向量组
也线性无关.
证明:
设有
使
,
即
,
因为
线性无关,
故有
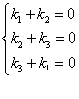
此线性方程组只有零解
,
也即向量组
线性无关.
定理
9.1
向量组
线性相关的充分必要条件是其中至少有一个向量可以由其余
个向量线性表示
.
证明:
必要性
设
线性相关,
即存在一组不全为零的数
,
使得
.
不妨设
,
则有
,
即
可以由其余
个向量
线性表示.
其实,
在向量等式
中,
任何一个系数
的向量
都可以由其余
个向量线性表示
.
充分性
设向量组
中有一个向量能由其余
个向量线性表示
.
不妨设
,
则
,
因为
不全为零,
所以
线性相关.
二、向量组线性相关和线性无关判别定理 :
设矩阵
的列向量组为
,
矩阵
的列向量组为
,其中矩阵
是通过对矩阵
做行初等变换后得到的.我们有以下定理:
定理
9.2
向量组
与向量组
有相同的线性相关性.
证明
:记
.那么,当且仅当齐次线性方程组
有非零解时向量组
线性相关.当且仅当齐次线性方程组
有非零解时向量组
线性相关.由于齐次线性方程组
或者只是对调了
的第
个方程与第
个方程的位置,或者只是用非零数
承
的第
个方程,或者只是把
的第
个方程的
倍加到第
个方程上去,这连个方程组一定是同解的,所以,对应的向量组
有相同的线性相关性.
定理
9.3
如果向量组
线性相关,那么
也线性相关.
证明
:向量组
线性相关,即存在不全为零的数
使
,
于是
,
但是
,
仍不全为零,因此,向量组
线性相关.
推论 9.4 线性无关向量组的任意一个非空部分组仍是线性无关向量组.
定理
9.5
设有
维向量组
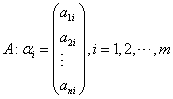
与
维向量组
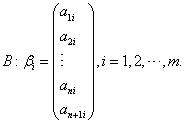
如果向量组
线性无关,那么,向量组
也线性无关.
推论
9.6
维向量组的每一个向量添加
个分量成为
维向量.如果
维向量组线性无关,那么,
维向量组也线性无关.反言之,如果
维向量组线性相关,那么,
维向量组也线性相关.
定义
9.2
在
型的矩阵
中,任取
行
列
,位于这些行列交叉处的
个元素,不改变它们在
中所处的位置次序而得的
阶矩阵行列式,称为矩阵
的
阶子式.
型矩阵
的
阶子式共有
个.
定理
9.7
设
维向量组
构成矩阵
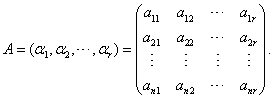
则向量组
线性无关的充分必要条件是矩阵
中存在一个不等于零的
阶子式.
推论
9.8
个
维向量组线性无关的充分必要条件是它们所构成的
阶矩阵的行列式不等于零.
推论
9.9
当
时,
个
维向量
必线性相关.
思考题：
1、 举例说明下列各命题是错误的
(1)
若向量组
线性无关，则
可由
线性表示;
(2)
若有不全为零的数
使
则
线性相关,
也线性相关;
(3)
若只有当
全为零时,
等式
才能成立
线性无关,
也线性无关;
(4)
若
线性相关,
也线性相关,
则有不全为零的数
,
使
同时成立.
2、 判断下列向量组是否线性相关 :
(1)
;
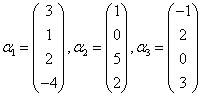(2)
;
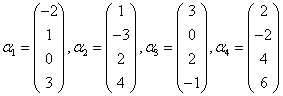(3)
;
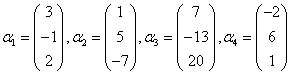(4)
.
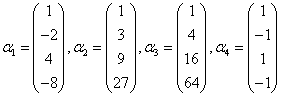3．
设向量组
线性无关,
讨论向量组
的线性相关性
.
4、
设向量组
线性无关,
线性相关,
则
必可由向量组
线性表示.
5 、选择题
(1)
维向量组
线性无关的充分必要条件是
A.
存在一组不全为零的数
,
使
;
B.
中任意两个向量都线性无关
;
C.
中存在一个向量
,
它不能由其他向量线性表示
;
D.
中任意一个向量都不能被其他向量线性表示
.
(2)
已知向量组
线性无关,
则向量组
A.
也线性无关;
B.
也线性无关;
C.
也线性无关;
D.
也线性无关.
(3)
设有任意两个
维向量组
与
.
如果存在两组不全为零的数
与
使
则
A.
与
.
线性相关;
B.
与
.
线性无关;
C.
线性无关;
D.
线性相关.